Python Programming
Lecture 14 Algorithm Intro
14.1 Algorithm Intro


- Complexity, Big-O (Searching)
- Recursion, D&C
- Sorting Algorithms
- Greedy Algorithm
-
Another stream of the basic knowledge about programming is algorithm and data structure.
- When two program solve the same problem but look different, is one program better than the other? (easy to read? easy to understand? execution time?)
-
An algorithm is a set of instructions for accomplishing a task.
-
Every piece of code could be called an algorithm.
-
To learn this, you only need to know some basic algebra and Discrete mathematics.
Binary Search (二分搜索)
-
Binary search is an algorithm; its input is a sorted list of elements. If an element you’re looking for is in that list, binary search returns the position where it’s located. Otherwise, binary search returns null.
-
Here's an example of how binary search works. I'm thinking of a number between 1 and 100.
-
You have to try to guess my number in the fewest tries possible. With every guess, I'll tell you if your guess is too low, too high, or correct.
-
Suppose you start guessing like this: 1, 2, 3, 4 ...
-
If you perform a simple search (简单搜索), and my number was 99, it could take you 99 guesses to get there!
-
Here's a better technique. Start with 50.
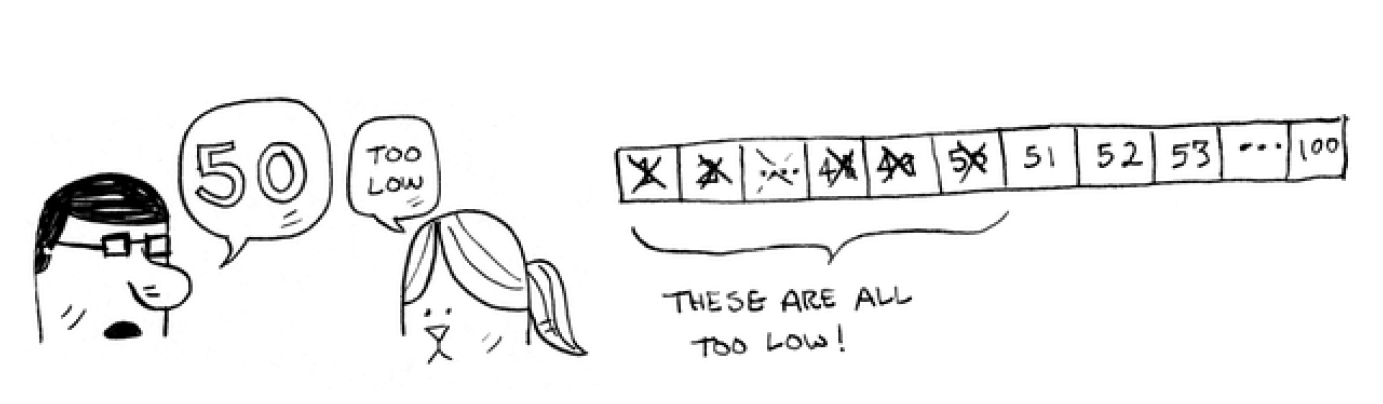

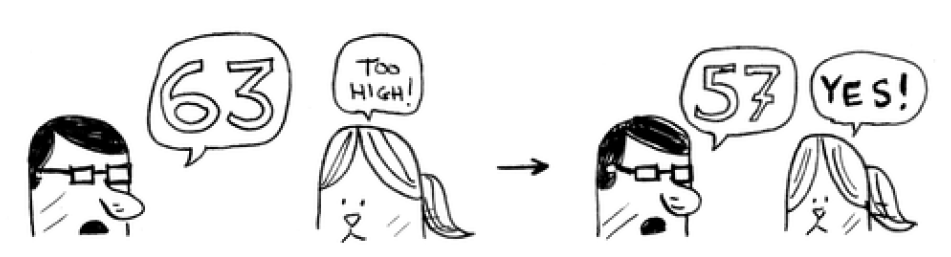

-
In general, for any list of $n$, binary search will take $log_2(n)$ steps to run in the worst case, whereas simple search will take $n$ steps.
-
Running time
-
Any time I talk about an algorithm, I'll discuss its running time. Generally you want to choose the most efficient algorithm— whether you're trying to optimize for time or space.
-
For simple search, the maximum number of guesses is the same as the size of the list. This is called linear time.
-
Binary search runs in logarithmic time.
Big O notation
-
Big O notation is special notation that tells you how fast an algorithm is.
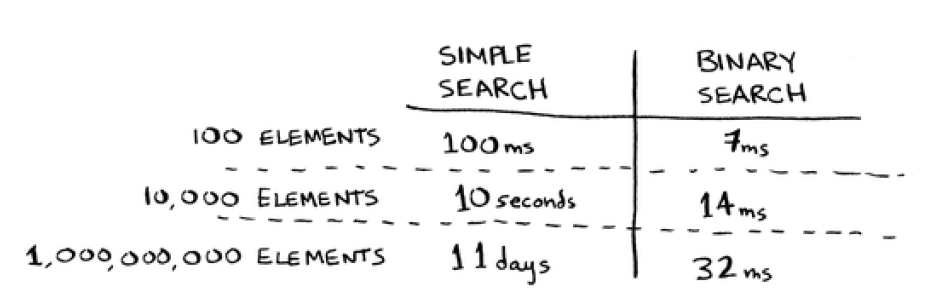
-
You need to know how the running time increases as the list size increases. That's where Big O notation comes in.
-
Big O notation tells you how fast an algorithm is. For example, suppose you have a list of size n. Simple search needs to check each element, so it will take n operations. The run time in Big O notation is $O(n)$.
-
Big O notation lets you compare the number of operations. It tells you how fast the algorithm grows. Run times grow at very different speeds.
-
Binary search needs $log(n)$ operations to check a list of size n. It's $O(log n)$.
-
Sometimes the performance of an algorithm depends on the exact values of the data rather than simply the size of the problem. For these kinds of algorithms we need to characterize their performance in terms of best case, average case and worst-case performance.
-
$O(log n)$, $O(n)$, $O(n * log n)$, $O(n^2)$, $O(2^n)$, $O(n!)$

14.2 Recursion
Recursion (递归)
-
Recursion is a method of solving problems that involves breaking a problem down into smaller and smaller subproblems until you get to a small enough problem that it can be solved trivially.
-
Recursion allows us to write elegant solutions to problems that may otherwise be very difficult to program.
- Base case and recursive case
-
The recursive case is when the function calls itself. The base case is when the function does not call itself again... so it doesn't go into an infinite loop.
def fact(n):
if n==1:
return 1 #Base case
else:
return n * fact(n - 1) #recursive case
Divide and Conquer (D&C, 分而治之)
-
D&C gives you a new way to think about solving problems. When you get a new problem, you don't have to be stumped. Instead, you can ask, "Can I solve this if I use divide and conquer?"
-
You want to divide this farm evenly into square plots. You want the plots to be as big as possible.
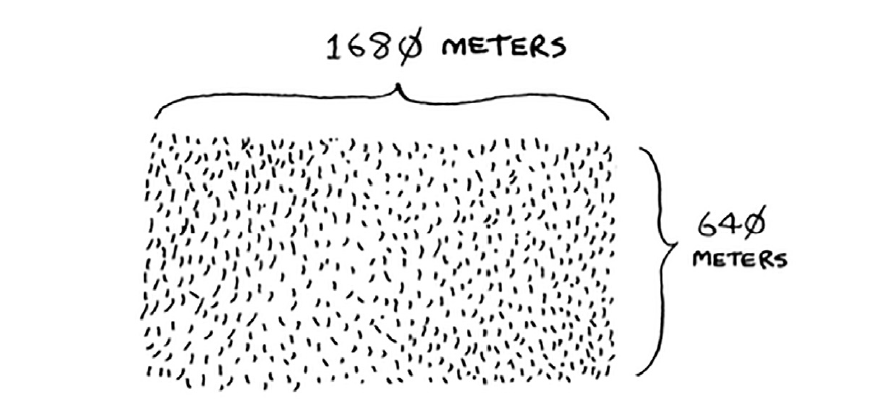

-
To solve a problem using D&C, there are two steps:
-
1. Figure out the base case. This should be the simplest possible case.
-
2. Divide or decrease your problem until it becomes the base case.
-
What is the largest square size you can use? You have to reduce your problem. Let’s start by marking out the biggest boxes you can use.

-
There's a farm segment left to divide. Why don't you apply the same algorithm to this segment?
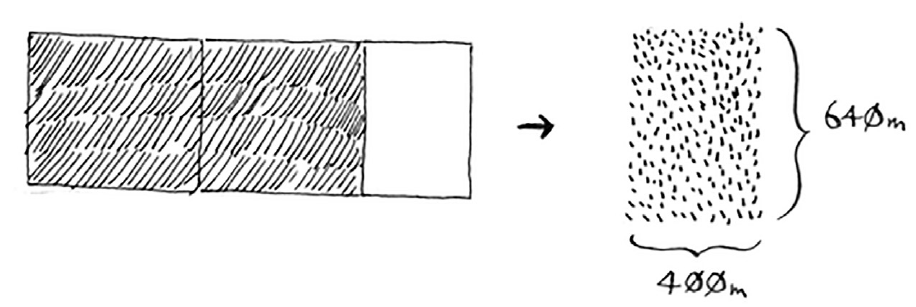
-
If you find the biggest box that will work for this size, that will be the biggest box that will work for the entire farm. You just reduced the problem from a 1680 × 640 farm to a 640 × 400 farm!
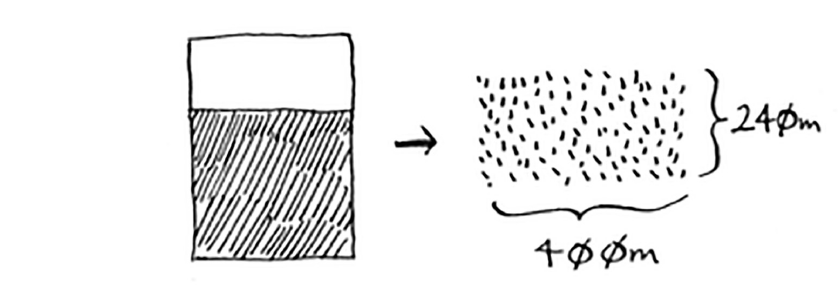
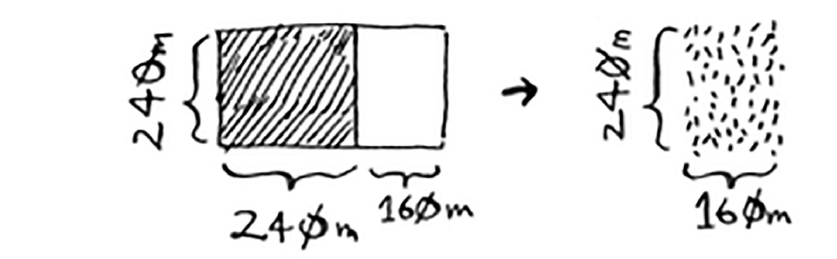
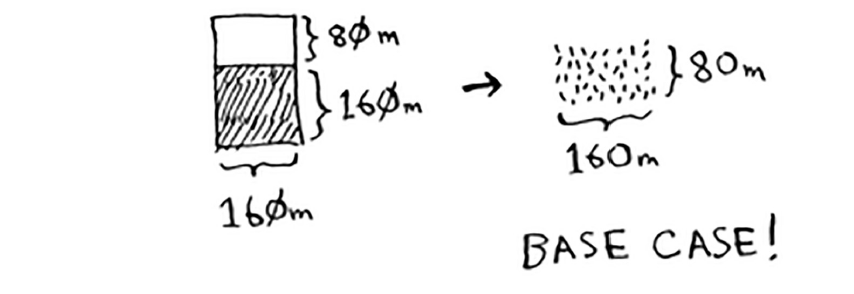
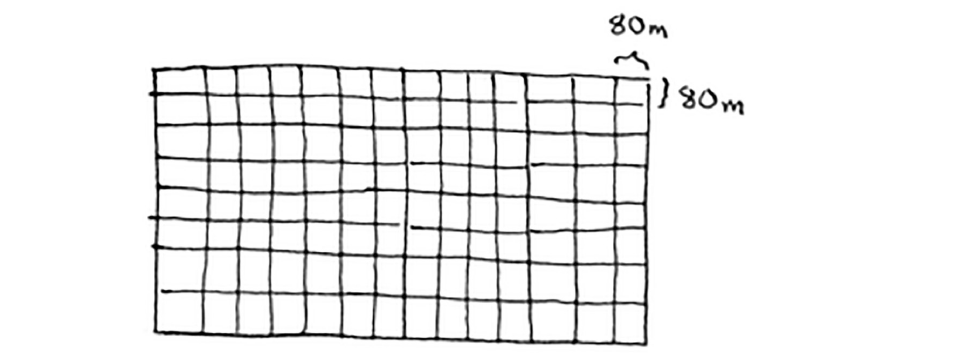
-
To recap, here's how D&C works:
-
1. Figure out a simple case as the base case.
-
2. Figure out how to reduce your problem and get to the base case.
-
D&C isn't a simple algorithm that you can apply to a problem. Instead, it's a way to think about a problem.
14.3 Recursion Examples
- Example 1: The Greatest Common Divisor
- We have learned a method to do it.
a = int(input('Enter your first number:'))
b = int(input('Enter your second number:'))
if a >= b:
x = a
y = b
else:
x = b
y = a
while y!=0:
r = y
y = x%y
x = r
print(x)
- Let's do it with recursion.
def gcd(a,b):
if b==0:
return a
else:
return gcd(b, a % b)
- Example 2: Fibonacci Numbers
- The Fibonacci Sequence is the series of numbers:
- 1, 1, 2, 3, 5, 8, 13, 21, 34, ...
def fib(n)
if n==0 or n==1:
return 1
else:
return fib(n-1)+fib(n-2)
- Example 3: Full Permutation
- There is a simple way...
import itertools
for j in itertools.permutations([2,5,6]):
print(j)
- Let's do it with recursion.
def recursion_permutation(list, first, last):
if first >= last:
print(list)
for i in range(first, last):
list[i], list[first] = list[first], list[i]
recursion_permutation(list, first+1, last)
list[i], list[first] = list[first], list[i]
x=[1,2,3,4]
recursion_permutation(x,0,len(x))
- Example 4: Hanoi
- The Tower of Hanoi is a mathematical game or puzzle. It consists of three rods and a number of disks of different sizes, which can slide onto any rod. The puzzle starts with the disks in a neat stack in ascending order of size on one rod, the smallest at the top, thus making a conical shape.
- The objective of the puzzle is to move the entire stack to another rod, obeying the following simple rules:
- Only one disk can be moved at a time.
- Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack or on an empty rod.
- No larger disk may be placed on top of a smaller disk.


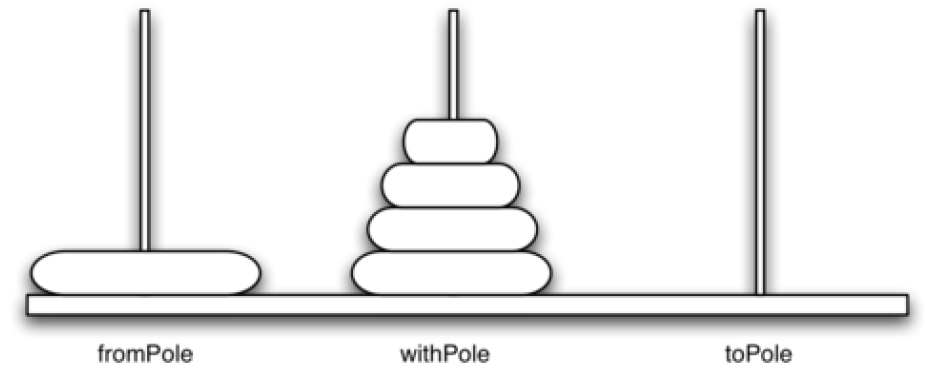
def moveTower(height, fromPole, toPole, withPole):
if height>=1:
moveTower(height-1,fromPole,withPole,toPole)
moveDisk(fromPole,toPole)
moveTower(height-1,withPole,toPole,fromPole)
def moveDisk(fp,tp):
print(f"moving disk from {fp} to {tp}\n")
Summary
- Algorithm Intro